
What’s beyond average roughness?
In surface texture, Average Roughness (Ra) is still the most widely used parameter, even though it has serious limitations. But what other tools are there that can tell us more about our surfaces? We’ll be exploring that topic in a series of posts, so watch this spot for updates every week! Let’s start with our

Surface Texture: meet the Scouts!
If you’re reading this blog, you know that we love sharing what we know about surfaces. Sometimes that information impacts people’s lives in the most unexpected of places! Brian Vogel is a Scout troop leader, in addition to his 30-year career in drafting and metrology. Though he’s amassed a wealth of GD&T and surface texture
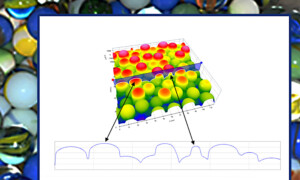
Losing our marbles?
Here’s a fun “macro” example of an important aspect of micro surface texture. Peak curvature is a measure of the “sharpness” of the small peaks in a surface. Many papers have been written on this important tribology parameter because it relates directly to a number of surface functions. But if you’re trying to estimate peak

Training Beyond School: Carl Musolff’s career as metallurgist, metrologist, and mentor
Engineers often wish there was a particular expert in the room to help them navigate the journey from problem to solution. For some very fortunate engineers, Carl Musolff has been that expert. Carl Musolff has made a career of solving challenging problems, for engines of every shape and kind. But what he really loves is
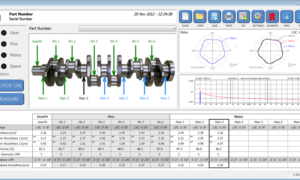
A power boost for your measurement system
Most measurement systems ship with software for acquiring data and displaying it in generalized ways. But what if you need to calculate special parameters, or display data in a way that’s unique to your process or application? Custom software tools, or “helper applications,” can pick up where off-the-shelf instrument software leaves off, filling in features

What am I missing when I only measure average roughness?
Here are two of our favorite pens: the “Uniball Grip” that we use with our logo, and the Pilot G-7 that we use for the Notepad Series. Both are relatively inexpensive, but they both write very well, and both grips feel great to hold. Speaking of “feeling great,” we put the pen grips under the
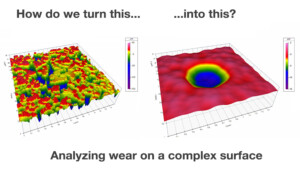
Where is the wear?
A joint post with Michigan Metrology. How would you measure the wear on this porous surface? This friction material was subjected to a laboratory wear test and measured by Michigan Metrology, using a Bruker NPFlex optical profiler. It has been worn at the center, and we need to know the depth of that wear
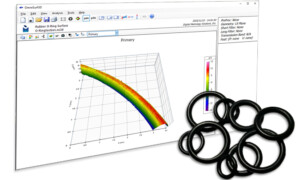
Measuring the surface of an O-ring
Here’s a challenging measurement. We want to look at the surface texture of this O-ring: With a small radius and cross-section, steep sides, and soft material, it’s almost impossible to measure with a stylus. An optical system can do the job, though. Here’s a measurement made with a Zygo ZeGage at 10X magnification, shown in

Are those valleys in my measurement data real?
Can I trust my measurement? Asking that question every time we measure drives us to be careful—and that keeps us producing meaningful results. Let’s look at a “simple” shop floor measurement of surface finish, made with a skidded instrument. And, let’s explore something that you might not imagine: “upward” dirt on the surface can cause
